Определение на разбиване:
Нека е даден граф G.
Разбиване е такова подмножество A от ребра на G, че всеки връх на G да попада в най-много едно ребро от A.

Определение на верига:
Нека е дадено разбиване A на графа G.
Верига ще наричаме такъв път в G, който не е цикъл и за който поредните ребра през едно са от разбиването A.

Определение на нарастваща верига:
Нарастваща верига за разбиването A на графа G е верига, за която крайните върхове не попадат в A.

Определение на максимално разбиване:
Разбиването A на графа G е масимално, когато съдържа повече (или равен брой) ребра от всяко друго разбиване на G.

Определение на двуделен граф:
Графът G е двуделен, ако множеството от върховете му се разбива на две подмножества - V_f (женски) и V_m (мъжки), така че краищата на всички ребра са в различни подмножества.

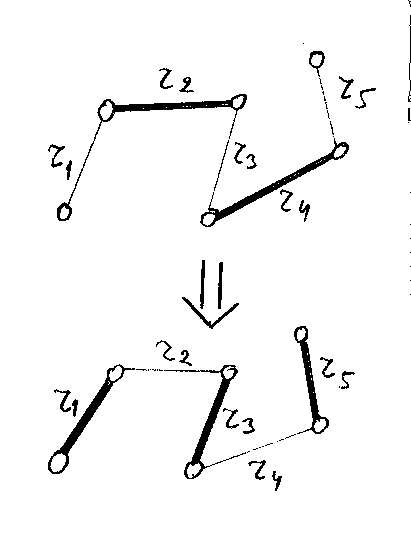
Лема за максималното разбиване (Chain_lemma): Нека е дадено разбиване A на графа G. Следните две твърдения са еквивалентни: (1) A е максимално разбиване. (2) Не съществува нарастваща верига за разбиването A. Доказателство: Първо да допуснем, че (1) е вярно, а (2) не е вярно, т.е. A е максимално разбиване и има нарастваща верига за A. Нека разгледаме ребрата r1,r2,...rk на някоя нарастваща верига. От определението на нарастваща верига следва, че нечетните ребра r1,r3,r5,...rk не са от A, а четните r2,r4,...rk-1 са. Очевидно броят k на ребрата във веригата е нечетно число, като ребрата от A са с едно по-малко от останалите. Нека обърнем ребрата по веригата така: махаме от A четните ребра и прибавяме нечетните (на рис. 1 е показано обръщане на примерна нарастваща верига от 5 ребра). Така ще получим ново разбиване A', което ще съдържа 1 ребро повече от A, т.е. A не е максимално разбиване. От достигнатото противоречие следва, че (1) => (2).