Минималното покритие съдържа максимално разбиване.
По-точна формулировка:
Нека C е минимално покритие на графа G.
Тогава съществува максимално разбиване A на G, което е подграф на C.
Доказателство:
От определението на покритие е ясно, че C е подграф на G, съдържащ всички му върхове. Да построим максимално разбиване на графа C, което да означим с B. Ще докажем, че B е максимално разбиване и за графа G.
Нека разделим ребрата на G на три групи така: червени ще наричаме ребрата от разбиването B. сини ще наричаме ребрата от покритието C, които не са от B. зелени ще наричаме останалите ребра на G, т.е. тези, които не са от C.
Ще направим анализ на свързаните парчета на графа C. Нека Z е едно такова парче.
(1) Във Z няма път, който да съдържа 3 или повече ребра. Ако допуснем че има път с поне три ребра, премахвайки второто ребро от пътя ще получим пак покритие на G, което ще има едно ребро по-малко от C, т.е. ще се окаже, че C не е минимално покритие.
(2) Ако във Z няма и пътища с 2 ребра, то очевидно Z ще се състои от единствено ребро. Ако пък във Z има път с 2 ребра и означим средният връх в този път със z, то всички останали върхове от Z ще бъдат свързани единствено със z, иначе ще получим противоречие с (1). В този случай ще наричаме Z звезда с център z.
(3) Във Z има единствено червено ребро, всички останали са сини. Ако във Z няма червено ребро, можем да боядисаме кое да е и ще получим ново, по-голямо разбиване от B. Ако пък има поне 2 червени ребра, от (2) следва, че те ще имат общ връх - центъра z на Z, което противоречи на факта, че B е разбиване.
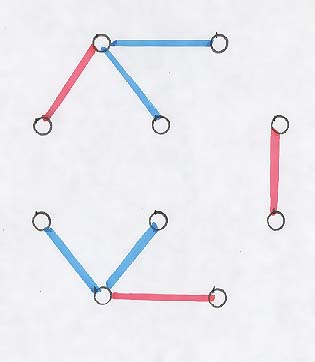
На рис. 1 е показан пример на минимално покритие C, съдържащо 7 ребра и неговото боядисване в синьо и червено.
Нека сега допуснем, че B не е максимално разбиване за G, т.е. в G има нарастваща верига за B. Нека ребрата във веригата са r1, r2 ... rk. От дефиницията на нарастваща верига следва, че k е нечетно, ребрата с четни номера са червени, а останалите не.
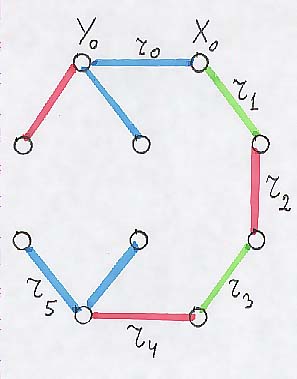
Оцветяването на вътрешните за веригата нечетни ребра r3, r5 ... rk-2 трябва да е зелено, иначе ще получим път с поне 3 ребра в C, което е невъзможно. На рис. 2 е показан граф G и нарастваща верига r1, r2 ... r5 за разбиването от предната рисунка.
Нека сега разгледаме крайното ребро в нарастващата верига r1. Има 2 варианта за оцветяването му:
- реброто r1 е синьо. Оставяме го така.
- реброто r1 е зелено. Първият му връх, който е краен за веригата да означим с X0. X0 трябва да е покрит от C, при това от единствено синьо ребро r0, иначе ще се окаже, че веригата не е нарастваща. Нека другият връх на r0 е Y0. От структурата на C знаем, че Y0 ще е покрит и от червено ребро. Правим следната манипулация: махаме r0 от C и вкарваме r1 в C. Ще получим пак покритие със същия брой ребра, но вече r1 е синьо.
В модифицираната нарастваща верига крайните ребра са сини, четните са червени, а вътрешните нечетни - зелени. Нека сега премахнем червените от C и да добавим зелените. Ще получим ново покритие C', което ще съдържа 1 ребро по-малко от старото. Това противоречие с минималността на C доказва теоремата.
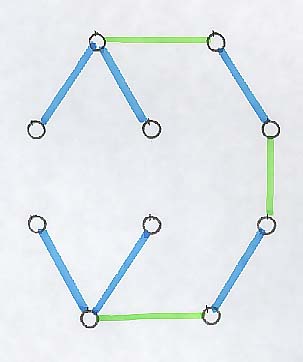
На рис. 3 е показан графа G и новото покритие C', съдържащо само 6 ребра.